|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IV.3. Взаимодействие плоскости
симметрии и параллельной ей трансляции.
Плоскости скользящего отражения
Рассмотрим сочетание двух операций
симметрии: отражения в плоскости симметрии
(операция 2-го рода) с параллельной ей трансляцией
- элементом симметрии бесконечных построек 1-го
рода [18]. Если произвольную фигуру 1 (рис.
22) отразить в зеркальной плоскости симметрии,
перпендикулярной оси X (mx), то получим
энантиоморфную ей фигуру 2. Трансляция 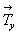  размножит
эти фигуры в направлении оси Y: из фигуры 1 получим
фигуру 3, затем 5, 7 и т.д., из фигуры 2 - фигуры 4, 6, 8 и
т.д. Для того чтобы перейти от фигуры 1 к фигуре 4,
необходимо произвести две последовательные
симметрические операции: отражение в зеркальной
плоскости mx и перенос на величину
вектора размножит
эти фигуры в направлении оси Y: из фигуры 1 получим
фигуру 3, затем 5, 7 и т.д., из фигуры 2 - фигуры 4, 6, 8 и
т.д. Для того чтобы перейти от фигуры 1 к фигуре 4,
необходимо произвести две последовательные
симметрические операции: отражение в зеркальной
плоскости mx и перенос на величину
вектора 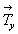 . В итоге
результирующим движением окажется скользящее
отражение, а следовательно, появится новый
элемент симметрии 2-го рода - плоскость
скользящего отражения, задающая две
простые симметрические операции: отражение в
плоскости симметрии и перенос в параллельном
заданной плоскости направлении на определенное
расстояние. Отсюда расположение фигур в данном
узоре (рис. 22, а) может быть
описано не только с помощью зеркальной плоскости
и вектора . В итоге
результирующим движением окажется скользящее
отражение, а следовательно, появится новый
элемент симметрии 2-го рода - плоскость
скользящего отражения, задающая две
простые симметрические операции: отражение в
плоскости симметрии и перенос в параллельном
заданной плоскости направлении на определенное
расстояние. Отсюда расположение фигур в данном
узоре (рис. 22, а) может быть
описано не только с помощью зеркальной плоскости
и вектора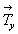 , но и с
помощью сложного элемента симметрии бесконечных
построек - плоскости скользящего отражения,
которая совпадает с плоскостью mx, т.е.
"работает" одновременно и как зеркальная
плоскость, и как плоскость скользящего
отражения. , но и с
помощью сложного элемента симметрии бесконечных
построек - плоскости скользящего отражения,
которая совпадает с плоскостью mx, т.е.
"работает" одновременно и как зеркальная
плоскость, и как плоскость скользящего
отражения.
Однако если порождающие элементы
симметрии (и зеркальную плоскость mx, и
трансляцию 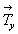 ) убрать, то
их произведение - плоскость скользящего
отражения - может сохраниться в качестве
самостоятельного элемента симметрии (рис.
22, б). В этом случае оба элемента симметрии,
задающие симметрические операции плоскости
скользящего отражения, окажутся "мнимыми" и не
существующими раздельно (т.е. операция отражения
задается мнимой зеркальной плоскостью), так же
как и вектор переноса является не реальной
трансляцией, а лишь трансляционной компонентой
этой плоскости. Однако реальная трансляция,
как основная симметрическая операция
кристаллического вещества, совсем исчезнуть не
может. В данном случае она сохранится,
трансформируясь в вектор, равный удвоенному
поступанию, т.е. ) убрать, то
их произведение - плоскость скользящего
отражения - может сохраниться в качестве
самостоятельного элемента симметрии (рис.
22, б). В этом случае оба элемента симметрии,
задающие симметрические операции плоскости
скользящего отражения, окажутся "мнимыми" и не
существующими раздельно (т.е. операция отражения
задается мнимой зеркальной плоскостью), так же
как и вектор переноса является не реальной
трансляцией, а лишь трансляционной компонентой
этой плоскости. Однако реальная трансляция,
как основная симметрическая операция
кристаллического вещества, совсем исчезнуть не
может. В данном случае она сохранится,
трансформируясь в вектор, равный удвоенному
поступанию, т.е. 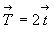 , тогда
как двукратно повторенные операции отражения в
плоскости скользящего отражения взаимно
уничтожатся, т.е. дадут операцию идентичности (m .
m = 1). Отсюда ясно, что величина
трансляционной компоненты плоскости
скользящего отражения всегда равна половине
реальной трансляции в этом направлении. , тогда
как двукратно повторенные операции отражения в
плоскости скользящего отражения взаимно
уничтожатся, т.е. дадут операцию идентичности (m .
m = 1). Отсюда ясно, что величина
трансляционной компоненты плоскости
скользящего отражения всегда равна половине
реальной трансляции в этом направлении.
Различают плоскости скользящего
отражения двух типов. К первому типу относятся
плоскости со скольжением вдоль одного из
координатных направлений. При этом буквами a, b
и с обозначаются плоскости со скольжением
вдоль координатных осей X, Y и Z соответственно. С
изменением ориентации трансляционной
компоненты меняются и обозначения этих
плоскостей. Графически вертикальные плоскости с
горизонтальным скольжением изображаются
штриховой линией (штрихи горизонтальны и
параллельны плоскости чертежа) (рис. 23,
а и 24, а), плоскости с
вертикальным скольжением (обычно вдоль оси Z) -
точечной линией (штрихи перпендикулярны
плоскости чертежа) (рис. 23, б и 24, а). Горизонтальные плоскости
обозначаются значками 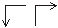 , стрелки на которых указывают направления
трансляционных составляющих (рис. 24,
а).
, стрелки на которых указывают направления
трансляционных составляющих (рис. 24,
а).
Плоскости 2-го типа характеризуются
трансляционными векторами, ориентированными
одновременно вдоль двух координатных
направлений (т.е. вдоль двух ребер элементарной
ячейки, см. с. 76), и, следовательно, результирующее
скольжение совпадает с диагональю грани (узловой
сетки) элементарной ячейки и образует косой угол
с координатными осями. Отсюда название таких
плоскостей скользящего отражения - клиноплоскости
(греч.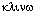 (клинос)
- косой). (клинос)
- косой).
Различают клиноплоскости двух видов.
Клиноплоскости n содержат трансляционные
компоненты, равные половинам координатных
трансляций 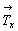 , , 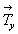 и и 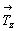 элементарной ячейки. Сам же
вектор скольжения соответствует половине
диагоналей "пустых" (нецентрированных) граней
элементарной ячейки: элементарной ячейки. Сам же
вектор скольжения соответствует половине
диагоналей "пустых" (нецентрированных) граней
элементарной ячейки: 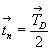 (где (где
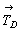 - диагональ грани
элементарной ячейки). Если же клиноплоскость
расположена параллельно центрированной грани
(сетке), то ее вектор скольжения оказывается
вдвое короче истинной трансляции, центрирующей
грань (сетку) ячейки, т.е. - диагональ грани
элементарной ячейки). Если же клиноплоскость
расположена параллельно центрированной грани
(сетке), то ее вектор скольжения оказывается
вдвое короче истинной трансляции, центрирующей
грань (сетку) ячейки, т.е. 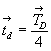 , и соответствует половине более короткой,
центрирующей данную грань трансляции. Такая
клиноплоскость обозначается буквой d 1 . , и соответствует половине более короткой,
центрирующей данную грань трансляции. Такая
клиноплоскость обозначается буквой d 1 .
В отличие от плоскостей a, b и с
клиноплоскости n и d не меняют своего
обозначения при изменении наименований
координатных осей. Графически клиноплоскости n
обозначаются штрихпунктиром (рис. 23,
в и 24, б), в обозначении же
плоскостей d каждый штрих заменяется
стрелкой, направление которой указывает на
увеличение вертикальной трансляционной
составляющей этой клиноплоскости (рис.
23, г и 24, в). Горизонтальные
клиноплоскости d и n обозначаются значком 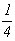  ,
где стрелка указывает направление скольжения, а
дробь - высоту плоскости в долях вертикальной
трансляции ячейки. ,
где стрелка указывает направление скольжения, а
дробь - высоту плоскости в долях вертикальной
трансляции ячейки.
|

