|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.4. Вывод пространственных групп
ромбической сингонии
При выводе пространственных групп
ромбической сингонии удобно использовать
основной принцип Вульфа о
фундаментальной роли плоскостей симметрии,
рассматривая их как порождающие элементы
симметрии, т.е. в качестве генераторов
пространственных групп.
Суть метода, предложенного Н.В.Беловым
[5, 18], наиболее ярко выступает при выводе групп
ромбической голоэдрии, так как ортогональный
координатный репер, максимальное число решеток
Браве и присутствие порождающих неэквивалентных
плоскостей симметрии, перпендикулярных всем
трем координатным направлениям, делает такой
вывод наиболее наглядным. Все это позволяет
распространить его и на вывод пространственных
групп остальных сингоний.
Вывод пространственных групп
ромбической голоэдрии
В качестве исходной при выводе
пространственных групп ромбической голоэдрии
возьмем точечную группу D2h ,
международный символ которой  подчеркивает топологическое
сходство всех трех неэквивалентных особых
направлений, что позволяет перенести акцент на
направления скольжения в плоскостях трех
позиций международного символа. Начнем вывод с
пространственных групп с примитивной решеткой. подчеркивает топологическое
сходство всех трех неэквивалентных особых
направлений, что позволяет перенести акцент на
направления скольжения в плоскостях трех
позиций международного символа. Начнем вывод с
пространственных групп с примитивной решеткой.
Пространственные группы с Р-решеткой
Сначала решим, какие трансляционные
разновидности плоскостей симметрии воз-можны на
каж-дой из трех позиций между-народного симво-ла
ромбической голоэдрии. При этом обратим внимание
на то, что плоскости скользящего от-ражения a, b
и с с трансляционной компонентой,
ориентированной вдоль одной из координатных
осей, изменяют свои наименования в зависимости
от той или иной ориентации их компонент ( ). Обозначения же
клиноплоскостей n не меняются в зависимости
от их ориентации относительно координатных
направлений вследствие того, что их
трансляционные компоненты направлены по
диагоналям граней элементарной ячейки, т.е. не
привязаны к какой-либо определенной
координатной оси. Таким образом, перпендикулярно
оси X, т.е. на 1-й позиции международного символа,
могут раполагаться плоскости m, n, c или
b; на 2-й позиции - перпендикулярно оси Y -
плоскости m, n, c или a и на 3-й -
перпендикулярно оси Z - плоскости m, n, a
и b. И вывод групп ромбической голоэдрии
сведется к определению сочетаний всех возможных
перечисленных выше плоскостей. Однако
формальная перестановка букв приведет к
большому количеству групп, значительно
превышающему их реальное число из-за того, что
одна и та же группа в разных аспектах будет
обозначаться разными символами (рис.
70). Избежать указанных трудностей можно,
воспользовавшись рекомендациями Н.В.Белова,
предложившего следующую схему их вывода. ). Обозначения же
клиноплоскостей n не меняются в зависимости
от их ориентации относительно координатных
направлений вследствие того, что их
трансляционные компоненты направлены по
диагоналям граней элементарной ячейки, т.е. не
привязаны к какой-либо определенной
координатной оси. Таким образом, перпендикулярно
оси X, т.е. на 1-й позиции международного символа,
могут раполагаться плоскости m, n, c или
b; на 2-й позиции - перпендикулярно оси Y -
плоскости m, n, c или a и на 3-й -
перпендикулярно оси Z - плоскости m, n, a
и b. И вывод групп ромбической голоэдрии
сведется к определению сочетаний всех возможных
перечисленных выше плоскостей. Однако
формальная перестановка букв приведет к
большому количеству групп, значительно
превышающему их реальное число из-за того, что
одна и та же группа в разных аспектах будет
обозначаться разными символами (рис.
70). Избежать указанных трудностей можно,
воспользовавшись рекомендациями Н.В.Белова,
предложившего следующую схему их вывода.
Первое семейство пространственных
групп составляют комбинации "удобных" - не
меняющих свое наименование - плоскостей
симметрии:
 и и  . .
Обратим внимание на то, что при записи
символов групп в стандартном аспекте
единственную в своем роде плоскость принято
располагать горизонтально, т.е. помещать на 3-ю
позицию символа.
Следующее семейство составят
пространственные группы с двумя "удобными"
плоскостями m и n и одной "неудобной"
на третьей позиции символа. При этом
"удобной" окажется плоскость с
горизонтельным скольжением (поскольку
вертикальное скольжение у горизонтальной
плоскости невозможно!):
 (рис.
71, а), (рис.
71, а),
 , ,

 (рис
71, б). (рис
71, б).
Как видим, каждая из двух первых групп
имеет своего топологического напарника. Однако
стандартный аспект в Интернациональных таблицах
соответствует установке с плоскостью а на
последнем месте символа. Во второй паре групп ( и и  ) вектор скольжения плоскости а,
расположенный в пр. гр. Pmna перпендикулярно к
плоскости m и в пр. гр. Pnma - перпендикулярно
клиноплоскости n (рис. 71, б),
делает эти группы топологически разными. ) вектор скольжения плоскости а,
расположенный в пр. гр. Pmna перпендикулярно к
плоскости m и в пр. гр. Pnma - перпендикулярно
клиноплоскости n (рис. 71, б),
делает эти группы топологически разными.
Иногда описание той или иной
кристаллической структуры дается в
нестандартной установке. В этом случае на помощь
приходит символ Шенфлиса, где надстрочный
порядковый номер группы в пределах одного
кристаллографического класса указывает на
определенную пространственную группу, выполняя
роль своеобразного ключа. Например, структура PdCl2
часто описывается в аспекте Pbnm (= Pnma =  ). ).
В третьем семействе пространственных
групп, с одной "удобной" плоскостью (m или n)
на последнем месте символа, две другие плоскости
могут быть либо однотипными, т.е. обе с
вертикальным или обе сгоризонтальным
скольжением:
 (рис.
72, а, б), либо разного типа - одна с
горизонтальным, другая с вертикальным
скольжением: (рис.
72, а, б), либо разного типа - одна с
горизонтальным, другая с вертикальным
скольжением: 
В последнем, четвертом
семействе пространственных групп нет ни одной
"удобной" плоскости, т.е. ни m, ни n. При
этом в одном варианте векторы скольжения двух
плоскостей параллельны друг другу и
перпенди-кулярны вектору 3-й плоскости:
Pcca (= Pbaa = Pbab = Pccb = Pbcb =Pcaa)
= =  (рис. 72,
в), в др-гом - векторы скольжения плоскостей
сим-метрии всех трех позиций символа взаимно
перпендикулярны ( со скольжением вдоль осей X, Y и
Z): (рис. 72,
в), в др-гом - векторы скольжения плоскостей
сим-метрии всех трех позиций символа взаимно
перпендикулярны ( со скольжением вдоль осей X, Y и
Z):
Pbca (= Pcab) =  (рис. 72, г). (рис. 72, г).
В итоге получено 16 пространственных
групп ромбической голоэдрии с Р-решеткой.
Каждая пара плоскостей в символе
ромбической голоэдрии задает характер и
положение результирующей оси 2-го порядка,
расположэенной параллельно линии пересечения
плоскостей и фиксированной на не занятой
плоскостями позиции символа. Причем, если обе
порождающие плоскости зеркальные или обе
содержат параллельные трансляционные векторы,
то возникшая ось окажется поворотной. Если же
вектор, параллельный оси, содержится лишь в одной
из плоскостей, он меняет характер оси на
винтовой. Таким образом, каждый символ
ромбической группы может быть записан в
развернутом виде:

Не следует также забывать, что любая
пара элементов симметрии любой позиции
развернутого символа (ось 2-го порядка и
перпендикулярная к ней плоскость симметрии)
обусловит появление и центра инверсии.
Пространственные группы с С-решеткой
Топологическая эквивалентность всех
трех направлений ромбо-бипирамидального класса mmm
делает центрировки А, В и С
неразличимыми. Однако центрировка одной пары
граней элементарной ячейки (в стандартной
установке - центрировка С) делает
горизонтальную плоскость топологи-чески
отличной от двух других, в данном случае от
вертикаль-ных плоскостей (1-й и 2-й позиций
символа), так как вектор 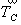 по-разному ориентирован относительно
горизон-тальной и вертикаль-ных плоскостей
(ле-жит в горизонтальной плоскости и распо-ложен
под косыми углами к вертикальным) и поэтому
по-разному с ними взаимодействует (рис.
73, а).
по-разному ориентирован относительно
горизон-тальной и вертикаль-ных плоскостей
(ле-жит в горизонтальной плоскости и распо-ложен
под косыми углами к вертикальным) и поэтому
по-разному с ними взаимодействует (рис.
73, а).
Для того чтобы найти результат
взаимодействия вектора 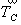 с вертикальными плоскостями, удобно разложить
его на две компоненты
с вертикальными плоскостями, удобно разложить
его на две компоненты  и и
 (рис. 73, ),
каждая из которых параллельна одной и
перпендикулярна другой плоскости. Плоскость
симметрии, получив горизонтальное скольжение от
1-й параллельной ей компоненты ( (рис. 73, ),
каждая из которых параллельна одной и
перпендикулярна другой плоскости. Плоскость
симметрии, получив горизонтальное скольжение от
1-й параллельной ей компоненты ( 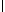 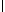 ) и изменив тем самым свое
наименование, будет перенесена в направлении 2-й,
перпендикулярной к ней компоненты ( ) и изменив тем самым свое
наименование, будет перенесена в направлении 2-й,
перпендикулярной к ней компоненты ( ) на ее середину. Таким образом, в
базоцентрированной решетке (С) появятся как бы
"вложенные" плоскости симметрии, т.е. будет
наблюдаться чередование плоскостей на 1-й и 2-й
позициях: m(g) 1 и с(n). ) на ее середину. Таким образом, в
базоцентрированной решетке (С) появятся как бы
"вложенные" плоскости симметрии, т.е. будет
наблюдаться чередование плоскостей на 1-й и 2-й
позициях: m(g) 1 и с(n).
Совсем иначе ведут себя
горизонтальные плоскости (3-й позиции символа) m,
n, a, b, взаимодействие которых с
лежащим в них вектором 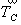 обусловит тождественное равенство плоскостей m
обусловит тождественное равенство плоскостей m
 n и a n и a  b, т.е . одна
и та же плоскость будет одновременно "работать"
в качестве плоскости как одного, так и другого
наименования. b, т.е . одна
и та же плоскость будет одновременно "работать"
в качестве плоскости как одного, так и другого
наименования.
Итак, в базоцентрированных группах
ромбической голоэдрии дополнительная
трансляция 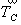 обусловит
следующие чередования: обусловит
следующие чередования:
на 1-й позиции символа m(b) и c(n),
на 2-й позиции символа m(a) и c(n),
на 3-й позиции символа тождественное
равенство m  n и a n и a  b. b.
Отсюда получим 6 базоцентрированных
групп ромбической голоэдрии:

В стандартной записи этих групп
предпочтение отдается не клиноплоскостям n, а
плоскостям с с однозначным скольжением вдоль
вертикальной оси Z, так же как плоскостям а, а
не b, на 3-й позиции символа. Например, Сс(n)c(n)a b = Ccca. b = Ccca.
Не следует забывать и о присутствии
осей 2-го порядка, порожденных каждой парой
пересекающихся плоскостей симметрии и затемс
взаимодействующих с вектором 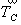 , что удваивает их количество. При этом,
если горизонтальные оси 1-й и 2-й позиций меняют
свой характер за счет косо расположенного к ним
центрирующего вектора , что удваивает их количество. При этом,
если горизонтальные оси 1-й и 2-й позиций меняют
свой характер за счет косо расположенного к ним
центрирующего вектора 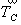 ,
то количество вертикальных осей (осей 3-й позиции)
удваивается без изменения их наименования.
Например, развернутый символ пр. гр. Ссса
запишется следующим образом: ,
то количество вертикальных осей (осей 3-й позиции)
удваивается без изменения их наименования.
Например, развернутый символ пр. гр. Ссса
запишется следующим образом: 
Пространственные группы с I-решеткой
В объемноцентрированных группах
ромбической голоэдрии присутствие
дополнительного вектора  , одинаково расположенного ко всем
порождающим плоскостям, не только сделает их
топологически эквивалентными, но и обусловит
обязательное чередование разноименных
плоскостей симметрии: m(n) и плоскостей со
скольжением вдоль одного ребра ячейки с
плоскостями со скольжением вдоль
перпендикулярного ребра. Действительно,
разложив вектор, центрирующий объем
элементарной ячейки на три координатных
составляющих , одинаково расположенного ко всем
порождающим плоскостям, не только сделает их
топологически эквивалентными, но и обусловит
обязательное чередование разноименных
плоскостей симметрии: m(n) и плоскостей со
скольжением вдоль одного ребра ячейки с
плоскостями со скольжением вдоль
перпендикулярного ребра. Действительно,
разложив вектор, центрирующий объем
элементарной ячейки на три координатных
составляющих  (рис. 73, б), увидим, что заданная
плоскость любой позиции символа, например mx,
за счет взаимодействия с двумя параллельными ей
векторами превращается в плоскость nx : mx
. (рис. 73, б), увидим, что заданная
плоскость любой позиции символа, например mx,
за счет взаимодействия с двумя параллельными ей
векторами превращается в плоскость nx : mx
.  . .
 = nx, которая, в
свою очередь, за счет взаимодействия с
перпендикулярным к ней вектором = nx, которая, в
свою очередь, за счет взаимодействия с
перпендикулярным к ней вектором  окажется на его середине. В
результате плоскость mx будет
чередоваться с плоскостью nx: mx(nx).
Плоскость 2-й позиции, например ay (= my
. окажется на его середине. В
результате плоскость mx будет
чередоваться с плоскостью nx: mx(nx).
Плоскость 2-й позиции, например ay (= my
.  ),
взаимодействуя с составляющими ),
взаимодействуя с составляющими  и и  ,
превратится в плоскость сy, которая под
действием ,
превратится в плоскость сy, которая под
действием  перенесется
на его середину, обусловив этим чередование
вдоль оси Y плоскостей ay(cy),
плоскость 3-й позиции az . перенесется
на его середину, обусловив этим чередование
вдоль оси Y плоскостей ay(cy),
плоскость 3-й позиции az .  . .  = bz и далее
bz . = bz и далее
bz .  --> az(bz). --> az(bz).
Таким образом, имея на 1-й позиции
символа - m(n) и b(c),
на 2-й позиции символа - m(n) и a(b),
на 3-й позиции символа - m(n) и a(b),
можно составить 6 комбинаций элементов
симметрии - 6 пространственных групп: Immm, Imma, Imam,
Imaa, Ibam, Ibaa. Однако не все они оказываются
оригинальными. К примеру, символы Imma и Imam (рис. 74, а), Ibam и Imaa (рис. 74, б) представляют одну и ту
же группу в разных аспектах.
В результате получим 4
пространственные группы ромбической голоэдрии с
I-решеткой:
Immm =  , ,
Ibam (=Imaa) =  , ,
Ibca (= Ibaa) =  , ,
Imma =  . .
Стандартная запись группы Ibca =
Ib(c)a(c)a(b) фиксирует такой ее аспект, при котором
векторы записанных в символе трех плоскостей
симметрии располагаются параллельно всем трем
координатным осям. Развернутая же запись всех
перечисленных выше I-групп будет включать в
себя и оси 2-го порядка. При этом помимо осей,
порожденных исходными плоскостями, появятся и
оси иного характера как результат
взаимодействия исходных осей с вектором  . Например, развернутый
символ группы Ibam будет иметь следующий вид: . Например, развернутый
символ группы Ibam будет иметь следующий вид:  . .
Пространственные группы с F-решеткой
Гранецентрированная ромбическая
решетка характеризуется тремя дополнительными
трансляциями, каждая из которых лежит в
плоскости одной из граней элементарной ячейки и
косо расположена по отношению к двум другим. Это
делает все три координатные плоскости
топологически эквивалентными. Однако все три
вектора  , ,  и и  (cм. рис. 73, в) взаимосвязаны, так как
центрировка двух граней элементарной ячейки
приводит к центрировке третьей ее грани: (cм. рис. 73, в) взаимосвязаны, так как
центрировка двух граней элементарной ячейки
приводит к центрировке третьей ее грани:  + +  = =  . Поэтому
достаточно рассмотреть взаимодействие
плоскости симметрии, заданной на одной из
позиций символа, лишь с двумя векторами F-решетки. . Поэтому
достаточно рассмотреть взаимодействие
плоскости симметрии, заданной на одной из
позиций символа, лишь с двумя векторами F-решетки.
Плоскость 1-й позиции mx при
взаимодействии с лежащим в ней вектором  станет одновременно и
клиноплоскостью nx (mx станет одновременно и
клиноплоскостью nx (mx  nx).
Взаимодействие же этих (m и n) плоскостей с
вектором nx).
Взаимодействие же этих (m и n) плоскостей с
вектором  = =  + +  поменяет
за счет присутствия в нем вертикальной
составляющей поменяет
за счет присутствия в нем вертикальной
составляющей  их
наименования: m на с, n на b, т.е.
плоскость с станет тождественно равной b (c их
наименования: m на с, n на b, т.е.
плоскость с станет тождественно равной b (c
 b), и
за счет взаимодействия с перпендикулярной к ней
компонентой b), и
за счет взаимодействия с перпендикулярной к ней
компонентой  окажется
на ее середине. Взаимодействие заданной
плоскости с вектором окажется
на ее середине. Взаимодействие заданной
плоскости с вектором  ничего нового не даст. Таким образом, задание на
любой позиции символа плоскости m влечет за
собой весь спектр плоскостей: m
ничего нового не даст. Таким образом, задание на
любой позиции символа плоскости m влечет за
собой весь спектр плоскостей: m   n (c n (c  b). В результате получим одну
пространственную группу b). В результате получим одну
пространственную группу
 = Fmmm = Fm = Fmmm = Fm  n(c n(c  b) m b) m  n(c n(c  a) m a) m  n(a n(a  b). b).
Однако следует помнить, что
параллельно центрированной грани элементарной
ячейки может располагаться "алмазная"
клиноплоскость d. А так как результатом
взаимодействия двух взаимно перпендикулярных
плоскостей симметрии будет ось 2-го порядка -
поворотная или винтовая, нетрудно прийти к
выводу, что перпендикулярно к плоскости d
может располагаться исключительно плоскость d,
ибо только в этом случае возникнут оси 2 или 21.
Поворотная ось 2-го порядка появится в том случае,
если параллельные трансляционные составляющие
двух пересекающихся плоскостей d направлены
в противоположные стороны, т.е. "погасят" друг
друга  , и винтовая 21
- если составляющие трансляционные компоненты
взаимодействующих плоскостей d направлены в
одну сторону , и винтовая 21
- если составляющие трансляционные компоненты
взаимодействующих плоскостей d направлены в
одну сторону  . Во всех
других вариантах взаимодействий плоскости d
с перпендикулярными к ней плоскостями иных
наименований (например, d . m, d . c, d
. n) возникли бы оси 2-го порядка с
недопустимой для них трансляционной
компонентой, равной 1/4 координатной трансляции.
Все это заставляет сделать вывод о
единственности голоэдрической группы с
"алмазными" плоскостями: Fddd = . Во всех
других вариантах взаимодействий плоскости d
с перпендикулярными к ней плоскостями иных
наименований (например, d . m, d . c, d
. n) возникли бы оси 2-го порядка с
недопустимой для них трансляционной
компонентой, равной 1/4 координатной трансляции.
Все это заставляет сделать вывод о
единственности голоэдрической группы с
"алмазными" плоскостями: Fddd =  . .
Вывод пространственных групп
ромбической гемиэдрии
Гемиморфные группы (см. с. 42),
подчиненные точечной группе mm2, отличаются от
голоэдрических тем, что из трех особых
направлений одно, как правило, совмещаемое с
координатной осью Z, представлено осью симметрии,
а два других - нормалями к плоскостям симметрии.
Это делает топологически различными
вертикальное и горизонтальные особые
направления. Поэтому приходится отличать
центрировку грани А(В) от С, так как центрирующий
вектор оказывается по-разному ориентированным
относительно единственной оси 2-го порядка. Таким
образом, вместо одного типа С(А,В)-решетки
Браве в голоэдрических группах в гемиморфных
появятся две: А(В)-решетка и С-решетка.
Пространственные группы с Р-решеткой
Для вывода всех групп ромбической
гемиморфии с Р-решеткой за основу логично
было бы взять уже выведенные ранее
пространственные группы ромбической голоэдрии и
отбросить одну из порождающих плоскостей
симметрии. Однако в этом случае придется из 48 (16
. 3) вариантов сочетания букв выбрать 10
неповторяющихся, которые и составят нужное
семейство пространственных групп симметрии. Это
связано с тем, что из каждой голоэдрической
группы можно получить три подгруппы, подчиненные
точечной mm2.
Значительно проще осуществить вывод
гемиморфных пространст-венных групп аналогично
выводу голоэдрических, комбинируя плоскости с
разными типами скольжения первых двух позиций
символа (см. с. 46-49). Зная порождающие плоскости,
нетрудно определить и характер порожденных ими
осей 2-го порядка. В результате получим:
1) группу только с зеркальными
плоскостями симметрии - симморфную пр. гр. Pmm2 ( ); );
2) группы с одной зеркальной и одной
плоскостью скользящего отражения - Pmn21 ( ), Pmc21 ( ), Pmc21 ( ), Pma2 ( ), Pma2 ( ); );
3) группы с двумя плоскостями
скользящего отражения:
а) обе плоскости с одинаковым
скольжением (обе с горизонтальным, обе с
вертикальным скольжением либо обе
клиноплоскости n) - Pba2 ( ), Pcc2 ( ), Pcc2 ( ), Pnn2
( ), Pnn2
( , ,
б) обе плоскости с разным скольжением
- Pna21 ( ), Pnc2
( ), Pnc2
( ), Pca21 ( ), Pca21 ( ). ).
В результате без лишних повторений
получили 10 гемиморфных групп ромбической
сингонии с Р-решеткой, каждая из которых
может быть представлена в двух аспектах (ось 2
всегда направлена вдоль оси Z!), например Pma2 = Pmb2.
Однако стандартная установка соответствует
плоскостям а на 2-й позиции символа и m или n
- на 1-й позиции.
Пространственные группы с С-решеткой
Если в группах ромбической голоэдрии с
Р-решеткой плоскости всех трех позиций
символа топологически неразличимы, что
затрудняет переход от них к гемиморфным группам,
то в группах с базоцентрированной решеткой (С)
вектор  жестко
фиксирует горизонтальную плоскость симметрии -
плоскость 3-й позиции, перпендикулярную к
единственной оcи 2-го порядка, делая ее
топологически отличной от вертикальных
плоскостей. Это позволяет вывести гемиморфные
группы с С-решеткой простым отбрасыванием
плоскостей 3-й позиции из символов
базоцентрированных голоэдрических групп
симметрии, выведенных ранее: жестко
фиксирует горизонтальную плоскость симметрии -
плоскость 3-й позиции, перпендикулярную к
единственной оcи 2-го порядка, делая ее
топологически отличной от вертикальных
плоскостей. Это позволяет вывести гемиморфные
группы с С-решеткой простым отбрасыванием
плоскостей 3-й позиции из символов
базоцентрированных голоэдрических групп
симметрии, выведенных ранее:
 (см. с. 110). (см. с. 110).
К этому же результату можно прийти,
рассмотрев взаимодействия возможных плоскостей
симметрии 1-й и 2-й позиций символа с вектором  , как это было сделано выше
при выводе всех голоэдрических групп. , как это было сделано выше
при выводе всех голоэдрических групп.
Пространственные группы с А-решеткой
Для того чтобы вывести гемиморфные
группы ромбической сингонии с фигурирующей в
справочниках бокоцентрированной А-решеткой (В-решетка
с центрированной гранью В топологически ей
идентична), можно также воспользоваться
выведенными ранее С-группами ромбической
голоэдрии, предварительно переведя их в А-аспект
(каждый в двух установках) (рис. 75).Отбросив
горизонтальные плоскости (3-й позиции) из
голоэдрических групп обеих установок, приходим в
каждой из них к одному и тому же результату: к
четырем группам ромбической гемиморфии с А-решеткой.
В отличие от пространственных групп с С-решеткой,
где вертикальные плоскости (1-й и 2-й позиций)
топологически одинаковы по отношению к вектору  , в А-группах вектор , в А-группах вектор  , располагаясь в плоскости
1-й позиции, оказывается наклонным к другой
вертикальной плоскости (2-й позиции), что делает
их топологически различными. Это объясняет
тождественность (двойственность) плоскостей
симметрии, параллельных центрированной грани - m , располагаясь в плоскости
1-й позиции, оказывается наклонным к другой
вертикальной плоскости (2-й позиции), что делает
их топологически различными. Это объясняет
тождественность (двойственность) плоскостей
симметрии, параллельных центрированной грани - m
 n, c n, c  b, и
чередование плоскостей 2-й позиции - m(c) и a(n): b, и
чередование плоскостей 2-й позиции - m(c) и a(n):

Топологическая неэквивалентность
вертикальных плоскостей симметрии в А-решетках
делает недопустимой их перестановку на первых
двух позициях символа без соответствующего
изменения наименования решетки Браве, как это
возможно в С-группах. Например, Аma2 = Bbm2   Abm2 = Bma2.
И если в С-группах вектор Abm2 = Bma2.
И если в С-группах вектор  , перпендикулярный вертикальным осям 2-го
порядка, просто удваивает их количество, то в А-группах
дополнительная трансляция , перпендикулярный вертикальным осям 2-го
порядка, просто удваивает их количество, то в А-группах
дополнительная трансляция  , расположенная косо по отношению к этим
осям, обусловливает не только их чередование, но
и разноименность, т.е. 2(21). Отсюда
развернутые символы А-групп: , расположенная косо по отношению к этим
осям, обусловливает не только их чередование, но
и разноименность, т.е. 2(21). Отсюда
развернутые символы А-групп:
Ama2 = Am  n a(n) 2(21 ), n a(n) 2(21 ),
Amm2 = Am  n m(c) 2(21 ), n m(c) 2(21 ),
Abm2 = Ab  c m(c) 2(21 ), c m(c) 2(21 ),
Aba2 = Ab  c a(n) 2(21 ). c a(n) 2(21 ).
Пространственные группы с I-решеткой
Топологическая эквивалентность всех
трех плоскостей голоэдрических I-групп
относительно вектора  ,
центрирующего объем элементарной ячейки,
затрудняет переход от них к
объемноцентрированным группам ромбической
гемиморфии, так как наличие "вложенных"
плоскостей симметрии, т.е. чередования различных
по наименованию плоскостей всех трех позиций
символа, приводит при отбрасывании плоскостей
одной из позиций к большому числу вариантов, что
усложняет их анализ и установление различных
аспектов одной и той же пространственной группы.
Например, из группы Ibam можно вывести
следующие гемиморфные группы: ,
центрирующего объем элементарной ячейки,
затрудняет переход от них к
объемноцентрированным группам ромбической
гемиморфии, так как наличие "вложенных"
плоскостей симметрии, т.е. чередования различных
по наименованию плоскостей всех трех позиций
символа, приводит при отбрасывании плоскостей
одной из позиций к большому числу вариантов, что
усложняет их анализ и установление различных
аспектов одной и той же пространственной группы.
Например, из группы Ibam можно вывести
следующие гемиморфные группы:
Ib(c) a (c) m(n) 
Поэтому при выводе I-групп
ромбической гемиморфии удобнее воспользоваться
прямым перебором возможных на первых двух
позициях символа порождающих плоскостей
симметрии: на 1-й позиции - m(n), b(c); на 2-й
позиции - m(n), a(c). В результате получим сразу 3
группы, каждая из которых является надгруппой
нескольких групп с Р-решеткой:

Пространственные группы с F-решеткой
Переход от гранецентрированных групп
ромбической голоэдрии с топологически
эквивалентными плоскостями одинакового
наименования всех трех позиций символа к
гемиморфным F-группам не вызывает
затруднений, так как удаление горизонтальной
плоскости с сохранением всех возможных
сочетаний вертикальных плоскостей даст то же
самое количество F-групп с зеркальными и
алмазными плоскостями:
 = Fmm2 = Fm = Fmm2 = Fm  n(b n(b  c) m c) m  n(b n(b  c) 2(21
), c) 2(21
),
 = Fdd2 = Fd (d'
) d(d' ) 2(21). = Fdd2 = Fd (d'
) d(d' ) 2(21).
Вывод пространственных групп
ромбической осевой гемиэдрии
Топологическая эквивалентность трех
особых направлений ромбо-тетраэдрического
класса (222) делает центрировки А, В и С,
так же как и в ромбо-бипирамидальном классе (mmm),
неразличимыми. Поэтому, как и голоэдрические,
группы осевой гемиэдрии ромбической сингонии
обслуживаются четырьмя типами решеток Браве: Р,
С (А,В), I и F.
Пространственные группы с Р-решеткой
Все пространственные группы,
подчиненные точечной группе 222, легко
получить, выписав в развернутом виде  выведенные ранее Р-группы
ромбической голоэдрии и изъяв из них операции
2-го рода. В результате кроме симморфной пр. гр. Р222
( выведенные ранее Р-группы
ромбической голоэдрии и изъяв из них операции
2-го рода. В результате кроме симморфной пр. гр. Р222
( ) получим три
асимморфные пространственные группы - Р2221 ( ) получим три
асимморфные пространственные группы - Р2221 ( ), Р21 21 2 ( ), Р21 21 2 ( ), Р21 21 21 ( ), Р21 21 21 ( ): ):

Из каждой тройки выписанных в символе
пространственной группы осей 2-го порядка любые
две, расположенные под углом 90o одна к другой,
могут служить порождающими, третья же,
перпендикулярная к ним, окажется порожденной.
Обратим внимание, однако, на то, что одинаковые
порождающие пары осей приводят к появлению осей
разного характера: Р222 и Р2221 (Р21212
и Р212121). Это объясняется
тем, что в одном случае порождающие оси
пересекаются, в другом - скрещиваются. В
результате 6 вариантов взаимодействия
пересекающихся и скрещивающихся поворотных и
винтовых осей 2-го порядка реализуются в
выведенных выше четырех пространственных
группах. При этом, если порожденная ось
пово-ротная, то порождающие оси пересекаются,
если же порожденная - винтовая, то порождающие
оси скрещиваются независимо от их характера.
Пространственные группы с С-решеткой
Для того чтобы получить
пространственные группы с непримитивными
решетками Браве, необходимо ко всем операциям
каждой Р-группы приложить трансляцию
соответствующей решетки. При этом, если решетка
имеет косые трансляции по отношению к осям
симметрии, то всегда будет наблюдаться
чередование осей поворотных и винтовых - 2(21),
если же дополнительный вектор решетки
перпендикулярен к оси симметрии, то он, перенося
ось на свою середину, не изменит ее характер. В
результате получим

Как видим, принципиального различия
между этими двумя группами нет, так как оси 2z
в сокращенной записи этих групп указывают на то,
что одноименные оси 1-й и 2-й позиций символа
пересекаются:
 . .
Сокращенная запись этой
пространственной группы указывает на то, что
одноименные оси скрещиваются, а разноименные -
пересекаются.
Пространственные группы с I-решеткой
Поскольку оси 2-го порядка всех трех
позиций символа относительно дополнительного
вектора  топологически
эквивалентны, то вдоль диагоналей каждой грани
элементарной ячейки в I-группах будет
наблюдаться чередование перпендикулярных к ней
поворотных и винтовых осей 2-го порядка - 2(21).
Взяв за основу пространственные группы с Р-решеткой
и добавив к ним вектор топологически
эквивалентны, то вдоль диагоналей каждой грани
элементарной ячейки в I-группах будет
наблюдаться чередование перпендикулярных к ней
поворотных и винтовых осей 2-го порядка - 2(21).
Взяв за основу пространственные группы с Р-решеткой
и добавив к ним вектор  ,
получим ,
получим

Несмотря на то что в каждой из
полученных двух I-групп на всех позициях
символа наблюдается чередование осей 2(21),
эти группы различны: в пространственной группе I222
одноименные оси пересекаются, в группе I21 21
21 - скрещиваются. Это отражено в их
краткой условной записи. На эту же особенность
перечисленных групп указывает и их
происхождение.
Пространственные группы с F-решеткой
В F-решетке совокупность трех
векторов, центрирующих все грани элементарной
ячейки, приводит к тому, что в одной и той же
пространственной группе оказываются
реализованными все возможные сочетания осей 2-го
порядка: и поворотные, и винтовые оси и
пересекаются, и скрещиваются. Таким образом,
комбинации всех четырех Р-групп слились в
одну F-группу - F222 ( ). ).
Переход от голоэдрических
пространственных групп к гемиэдрическим (mmm -->
mm2, 222) подразумевает освобождение от операций
симметрии 2-го рода - плоскостей и (или) центров
инверсии. Естественно, воспользовавшись
обратным приемом, можно восстановить
голоэдрические группы, взяв за основу
гемиэдрические.
Легко увидеть, что результатом
последовательных отражений в трех плоскостях
симметрии любой пространственной группы класса mmm
будет инверсия. Положение центра инверсии
зависит от его взаимодействия с трансляционными
векторами исходных плоскостей скользящего
отражения, каждый из которых сдвигает точку
инверсии на свою середину. В результате этого
центр инверсии может оказаться в общем случае в
одной из восьми неэквивалентных позиций с
координатами  . Таким
образом, приняв за исходную одну из
гемиэдрических пространственных групп и выделив
в ней независимые позиции для центров инверсии,
можно получить все голоэдрические группы, для
которых исходная группа служит подгруппой. Если
инверсия добавляется к операциям непримитивных
пространственных групп, то число возможных
независимых позиций для точки инверсии
сокращается. Например, в гемиморфных группах с Р-решеткой
возможны лишь 4 позиции: . Таким
образом, приняв за исходную одну из
гемиэдрических пространственных групп и выделив
в ней независимые позиции для центров инверсии,
можно получить все голоэдрические группы, для
которых исходная группа служит подгруппой. Если
инверсия добавляется к операциям непримитивных
пространственных групп, то число возможных
независимых позиций для точки инверсии
сокращается. Например, в гемиморфных группах с Р-решеткой
возможны лишь 4 позиции:  , так как отсутствие фиксированного начала
координат вдоль оси Z делает тождественными
позиции 000 и , так как отсутствие фиксированного начала
координат вдоль оси Z делает тождественными
позиции 000 и  , ,  и и  и т.д. Расположив центры инверсии в этих
позициях и рассмотрев их взаимодействия с
исходными элементами симметрии группы Рmn21,
получим 4 голоэдрические группы: и т.д. Расположив центры инверсии в этих
позициях и рассмотрев их взаимодействия с
исходными элементами симметрии группы Рmn21,
получим 4 голоэдрические группы:
Pmn21 . i(00z) =
Pmna,
Pmn21 . i(0 1/4 z)
= Pmnn = Pnnm,
Pmn21 . i(1/4 0z) =
Pmnm = Pmmn,
Pmn21 . i(1/4 1/4 z)
= Pmnb = Pnma;
из группы Сmc21 получим только
две группы:
Cmc21 . i(00z)
= Cmcm,
Cmc21 . i(0 1/4 z)
= Cmca.
В пространственной группе Р222
различными для возможных центров инверсии
окажутся четыре позиции: 000,  , ,  и и  , располагая в которых центры
инверсии, получим следующие пространственные
группы ромбической голоэдрии: , располагая в которых центры
инверсии, получим следующие пространственные
группы ромбической голоэдрии:
Р222 . i(000) = Pmmm,
P222 . i(00 1/4) = Pccm,
P222 .i(1/4 1/4 0) = Pban,
P222 .i(1/4 1/4 1/4) = Pnnn.
Для пространственной группы I222
таких позиций для центров инверсии две - 000 и  : :
I222 . i(000) = Immm,
I222 . i(00 1/4) = Imaa = Iccm.
Указанным способом может быть
осуществлен переход от гемиэдрических групп к их
надгруппам ромбической голоэдрии. Конечно, в
качестве вводимой операции симметрии 2-го рода
можно использовать и отражение в плоскости
симметрии: горизонтальной, если исходной
является гемиморфная группа, и любой плоскости -
при выводе из групп осевой гемиэдрии.
| 
